Laban Movement Analysis in Max MSP. This project aims to make a use of motion capture data to control a digital music instrument. The idea is to create an instrument in Max MSP and use data from Leap Motion controller to control it.

Background

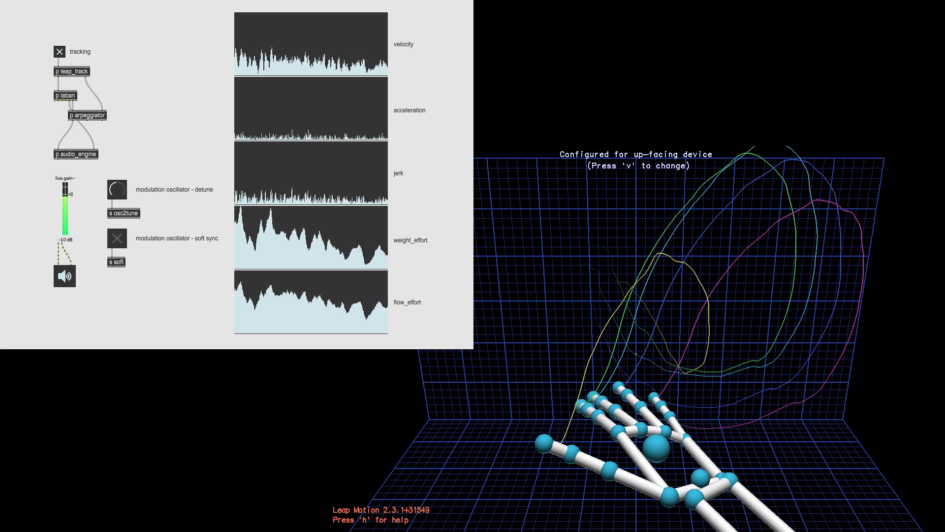
For this project I have created a synthesizer (equipped with a sequencer) that I could control by expressive hand gestures. My aim was to program an instrument that I can control by high-level movement descriptors. I have taken a simplified approach to Laban Movement Analysis (LMA). I have limited the LMA in this project to right-hand palm analysis only. Since the computation of LMA has proven to be challenging I have limited the implementation to computing low-level kinematics (velocity, acceleration, and jerk) and selected Laban Effort descriptors (Weight and Flow).

Implementation

I have programmed this project in Max MSP. Similarly like I have done in some of my previous projects I have decided to use Leap Motion Controller as an input device to capture the hand motion tracking data. I have used an additional leapmotion Max object from Ircam to receive Leap Motion Controller data. Since I was not able to find a Max implementation of LMA I have made an attempt at programing it from the ground up. My implementation is based on the review contained in C. Larboulette and S. Gibet.

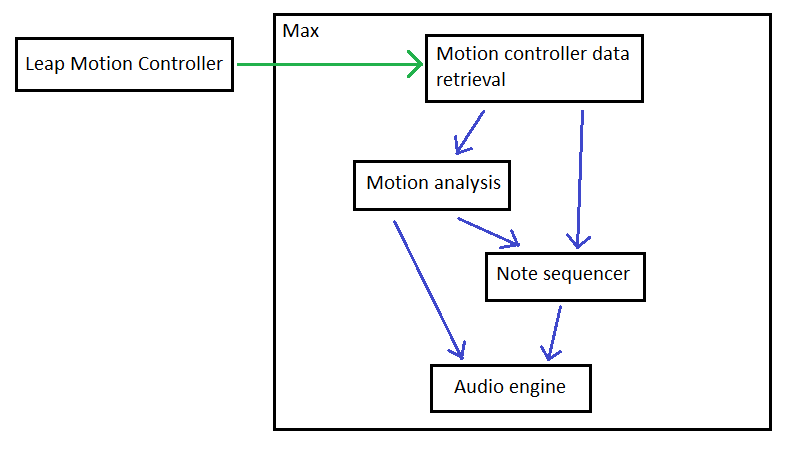
Motion controlled digital instrument block diagram
Block diagram of the projects building components

Motion controller data retrieval

The first step of the process happens inside the block responsible for the motion controller data retrieval. I have set it so that data from the Leap Motion Controller is received every 20 ms. Right-hand palm position is being filtered out from the overall retrieved data. Palm coordinates in the form of three numbers are being passed to the block responsible for motion analysis.

  • Laban Movement Analysis velocity
  • Laban Movement Analysis acceleration
Parts of the code responsible for the velocity scalar value (left) and for the acceleration scalar value (right) calculations

Motion analysis

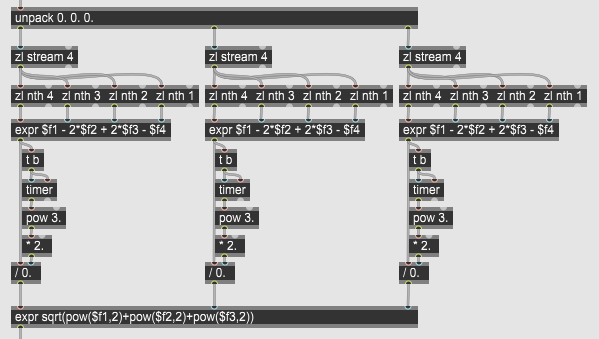
Next step of the process happens inside the motion analysis block. Palm coordinates are here used to calculate low-level kinematics (velocity, acceleration, and jerk) and two Laban Effort descriptors (Weight and Flow). The top half of the block contains parts responsible for computing velocity, acceleration, and jerk scalars. On their basis, the Weight and Flow Efforts are being calculated in the lower half. Flow Effort is being calculated based on the last 20 velocity values. Flow Effort is being calculated based on the last 20 jerk values. As the last stage within this block, all values are being scaled so that each of them will span within the 0-127 range. The scaling process has been automated – the highest generated value of each parameter is being taken as a maximal value in the calculation. This process is necessary because the remaining blocks have been build to accept only values from within this range.

  • Laban Movement Analysis jerk
  • Laban Movement Analysis weight and flow efforts
Parts of the code responsible for the jerk scalar value calculation (left) and for the calculation of Weight Effort and Flow Effort (right)

Note sequencer

The third building block contains the musical note sequencer. I have specifically created it for this project. Flow Effort value calculated in the previous block is being used to control it. I have made it so that this value is controlling the ’density’ of the notes generated by the sequencer and length of the notes. Each time the value drops to zero – new melody and gate sequences are being generated. An additional parameter from the motion controller data – hand presence – is also being used in this block. This parameter is being used to create a smoothing effect in case the hand goes in or out of the motion controller field of view.
I have decided to add rhythmical parts (kick drums and hi-hat) that I have also included inside this module. The kick drum is being triggered every fourth step of the melody sequencer. Euclidean rhythm generator is controlling the hi-hat. The rrhythm generator which is also dependant on the Flow Effort value.

Audio engine

The last building block contains the audio engine. When I creating the engine (monophonic synthesizer) I have taken inspiration from Don Buchla’s 259 complex oscillator. Note sequencer is controlling the melody played by the synthesizers. Weight Effort is controlling the characteristic of the audio – depth of the synthesizers phase modulation.

The result